Lógicamente

Empecemos con un pequeño ejercicio de razonamiento. Un viernes del mes de agosto. Un amigo me llama y me propone ir a la playa al día siguiente. Es verano y la probabilidad de precipitación es baja. No obstante, estamos en Burdeos así que nunca se sabe. Contesto que me apuntaré si hace buen tiempo. El sábado, mi amigo y yo estamos en la playa. ¿Hace buen tiempo? Veamos qué nos dice la lógica.

La verdad no siempre es intuitiva. Cometemos errores de razonamiento o falacias cada día. Por ejemplo, no es válido afirmar que la homeopatía es efectiva porque no se haya demostrado lo contrario (aunque en este caso, además, sí que se ha demostrado). Otro ejemplo sería afirmar que el SARS-CoV-2 es inofensivo y no corremos peligro porque así lo ha dicho un virólogo muy importante (argumento de autoridad o magister dixit).

Algunas falacias son cometidas intencionalmente y suelen tener fines oscuros. Otras son involuntarias y pueden deberse a la ignorancia, a la toma de atajos en el razonamiento o al exceso de confianza en la intuición. En cualquiera de los casos, las falacias no son buenas amigas. El pensamiento lógico es una herramienta esencial para la supervivencia del ser humano: la capacidad de razonar críticamente nos permite movernos en una sociedad compleja. La lógica ayuda al ser humano a satisfacer necesidades tan básicas como conseguir alimento o vivir bajo un techo.

Todo esto está muy bien. Pero no todo es supervivencia y bien individual. Si los cimientos de nuestro conocimiento actual son sólidos, no es sino gracias a la lógica utilizada a lo largo y ancho del planeta durante milenios. Si podemos caminar a hombros de gigantes y no empezar de cero con cada generación, es gracias a la solidez que nos proporciona la lógica, cuyos principios son simples (por ejemplo si tengo A, entonces no tengo B: tengo B, entonces no puedo tener A) pero no siempre son tenidos en cuenta en nuestro día a día.

Ya has tenido tiempo suficiente para pensar una respuesta para el pequeño ejercicio de razonamiento inicial. ¿Hace buen tiempo en Burdeos? Si tu respuesta es que sí, estás cometiendo un error de razonamiento conocido como “afirmación del consecuente”. Si descomponemos el problema, tenemos las siguientes premisas:

• Si hace buen tiempo, voy a la playa (si A, entonces B)
• Voy a la playa (B)

Afirmar que hace buen tiempo a partir del hecho de que se ha ido a la playa (si B, entonces A) es un error porque no hay ninguna premisa que implique este hecho. Hay muchas otras razones que pueden explicar que vaya a la playa (por ejemplo, un viejo amigo ha venido desde Estrasburgo y me insiste para que vayamos a pesar de la lluvia). A partir de estas premisas, no es válido afirmar que haga buen tiempo, pero tampoco es válido afirmar que no lo haga. La realidad es que no es posible sacar ninguna conclusión a partir de B. La única forma de concluir con respecto a la primera premisa (si A, entonces B), sería tener A (hace buen tiempo) como segunda premisa. En este caso, sí se puede afirmar B (voy a la playa) sin error.

Una persona que tiene mucho que contar con respecto a la lógica es Marcos López Aznar, licenciado en psicología y en filosofía, y próximamente doctor. Marcos lleva más de 20 años enseñando lógica: en lo que respecta al aprendizaje, sabe de lo que habla. Además, es el creador del diagrama de Marlo, una forma de representar silogismos intuitiva y fácilmente asimilable gracias a la cual es posible sacar conclusiones lógicas válidas evitando el riesgo de cometer falacias basándonos únicamente en la intuición. No dudes en visitar su sitio para más información: https://diagramademarlo.wordpress.com/.

La lógica a hombros de un gigante

Juan García Ruiz: ¿Cuándo y cómo nace el diagrama de Marlo?

Marcos López Aznar: Siempre me he sentido insatisfecho con los resultados en lógica de mis alumnos. Desde 2011 estuve haciendo diversas pruebas con diseños gráficos que pretendía utilizar para mejorar la comprensión de las cuestiones más abstractas que se afrontan en esta disciplina, convencido de que la imagen visual es la mejor herramienta para facilitar la captación de conocimiento. Así lo pensaba Aristóteles y así se desprende en Platón, que postulaba el conocimiento de los geómetras y el uso de imágenes como trampolín para la “aprehensión e intelección de las ideas puras”. Eso significa que no puede haber desarrollo del pensamiento abstracto si no partimos de bases tangibles. Primero ver y luego pensar, ese fue el principio que me movió a desarrollar diagramas lógicos.

JGR: ¿En qué consiste el diagrama de Marlo?

MLA: El diagrama de Marlo permite representar gráficamente, en modelos proposicionales, sentencias lógicas, de modo que una vez representadas podemos sintetizar las proposiciones en un solo modelo mediante procesos de síntesis. Esta síntesis se produce mediante la superposición de dos conjuntos. Por ejemplo, imaginemos el conjunto de los números terminados en cero (ce). Todos ellos son divisibles por dos (d) y todos ellos son divisibles por cinco (cin).

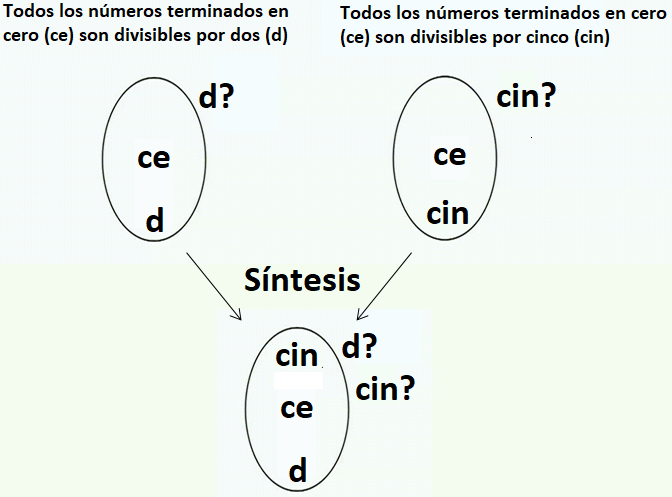
Si al representar ambas proposiciones tenemos en cuenta que al margen de los números terminados en cero hay, o puede haber otros números divisibles por dos (d?) y otros números divisibles por cinco (cin), al superponer los modelos proposicionales del número cero nos encontramos las siguientes asociaciones: Una parte de d y de cin quedan asociadas dentro del conjunto de ce, y luego tenemos fuera del conjunto de ce un tipo de d y un tipo de cin que no están ni asociados ni separados. Es decir, que una parte de los números divisibles por dos son divisibles por cinco (los que terminan en cero) y luego puede haber números que no terminan en cero fuera de ce que pueden o no ser divisibles por dos (d?) y/o por cinco (cin?).

JGR: ¿Cómo puede el diagrama de Marlo beneficiar el aprendizaje?

MLA: Cuando representamos las premisas en el diagrama de Marlo lo hacemos poniendo el sujeto en el centro de una figura geométrica, normalmente un círculo y tenemos que decidir si dividimos o no ese conjunto. Por ejemplo, en el conjunto de los andaluces algunos son sevillanos y otros no, y por eso tendríamos que dividir el círculo de los andaluces para separar a los sevillanos de los no sevillanos. Pero si cambiamos de perspectiva tenemos que reordenar la información de modo que ahora tenemos que en el conjunto de los sevillanos todos son andaluces, y por eso no hay que dividirlo. Pero lo interesante es que si hacemos las cosas bien nos tenemos que preguntar si fuera del conjunto de los sevillanos, en el espacio de los no sevillanos, debemos representar otros posibles andaluces. Una vez analizados los resultados que he obtenido en el aula con mis diagramas, estoy seguro de que reorganizar la información desde distintos puntos de vista, el de los andaluces y el de los sevillanos, es un ejercicio que favorece la flexibilidad mental. No tengo dudas de que el apoyo que supone la imagen para convertir una premisa del tipo Todo A es S en Algún A es S, sin olvidarse de otros posibles A que no son S, beneficia el desarrollo del pensamiento abstracto y lo pone al alcance de la mayoría.

Además, el desarrollo de los diagramas de Marlo, que no son otra cosa que una versión dinámica de los diagramas de Venn mejorada con las teorías de la cuantificación del predicado de Bentham, Hamilton, Jevons y otros autores del XIX, ha dado lugar a unos diagramas lógicos de árbol llamados redes de Expectativas Marlo en lo que podemos operar con números o con colores. Esto favorece lo que se llama razonamiento heterogéneo. Hay alumnos a los que se les dan fatal los números y las matemáticas, pero son capaces de razonar velozmente con colores y es algo que debemos potenciar, porque no todos los cerebros son iguales.

JGR: Hablemos de tu libro. Me lo leí en su tiempo y lo encontré muy pedagógico. ¿Estás contento con la acogida que recibió?

MLA: Me sorprendió que el libro llegó a estar en la lista de los más vendidos, y aunque eso no supone un gran número de ejemplares en nuestro país, sí recibió la suficiente difusión en los medios como para ser conocido en el mundo de habla hispana. De hecho, fue citado en varios periódicos y en importantes medios de las redes sociales. En este sentido, y teniendo en cuenta que el libro era autoeditado, estoy muy satisfecho con la difusión y con los comentarios de las personas que lo han leído. Sin embargo, escribí Cálculo lógico de modelos proposicionales (Lopez Aznar, 2014) hace seis años y aunque en lo esencial nada ha cambiado, son muchas las cosas que hemos aprendido en estos últimos seis años desarrollando una tesis doctoral a partir de ellos. Ahora los diagramas de Marlo tienen una base teórica potente, unos antecedentes históricos bien definidos y un desarrollo prometedor en forma de diagramas lógicos de árbol complementarios.

JGR: ¿Se sabe algo de la neurobiología que podría apoyar el diagrama de Marlo?

MLA: Los diagramas de Marlo son dispositivos de memoria externa que ayudan a mantener en la memoria de trabajo todas las variables en juego, y lo hacen de forma más evidente e intuitiva que los diagramas de Venn. En Venn hay que representar la totalidad del universo del discurso y eso pueden ser muchas intersecciones de círculos cuando hay más de tres variables. En Marlo representamos solo la información relevante que hay que tener en cuenta para no cometer falacias. Esto significa que potenciamos la memoria de trabajo sin exceder su capacidad, de modo que podemos interpretar los diagramas y realizar inferencias atendiendo a un número pequeño de relaciones. La neurobiología está de nuestro lado en la adecuación entre las capacidades cognitivas humanas y las exigencias de los diagramas como herramienta didáctica.

Mayor apoyo de la neurobiología tienen las redes de expectativa. Al igual que las redes neuronales, nuestras redes funcionan por procesos de excitación e inhibición que propagan la verdad y la falsedad por sus nodos. Además, el modo en el que se organizan los conjuntos en nuestras redes tiene una correspondencia muy interesante con el modo en el que se organizan en el lenguaje natural las relaciones entre los términos todos, ninguno, este concreto y alguno cualquiera. Y en cualquier caso, nuestros modelos de redes y nuestra forma de representar los conectores lógicos en ellas son muchísimo más simples y explican mucho más que sus predecesores, como los circuitos lógicos neuronales de McCulloch y Pitts de los años 90 o las redes neuronales de Hopfield. Hoy nos parece que todos los modelos lógicos de redes que hemos conocido son innecesariamente complejos.

JGR: Tengo entendido que el diagrama de Marlo ha hecho ruido al otro lado del Atlántico. ¿Estoy en lo cierto?

MLA: Me han escrito algunas personas desde Perú, México y Argentina que han leído mi libro para darme las gracias por difundir un método tan clarificador, lo cual es altamente gratificante. Mi página web ya ha recibido miles de visitas de toda Latinoamérica. Las visitas y la difusión del método me parecen muchas en términos relativos, considerando que se trata de una página de lógica y de un método heterodoxo creado por un profesor de secundaria. Sin embargo, la difusión y las visitas son pocas en términos absolutos todavía. Los diagramas de Venn siguen siendo los diagramas oficiales en todo el mundo. Tal vez después de publicar la tesis doctoral dentro de dos o tres meses el mundo universitario comience a hacerse eco de mis diagramas, pero a día de hoy son todavía una innovación con pocos adeptos.

JGR: ¿Cuáles son los próximos pasos para el diagrama de Marlo?

MLA: Después de defender la tesis doctoral me gustaría seguir escribiendo para difundir el método. Hace unos días recibí una propuesta de libro de una de las editoriales con peso en el mundo académico y tal vez me lance a ello, aunque sigo sin tener claro si será mejor para los diagramas publicar libros, artículos o simplemente mejorar la página web, porque de hecho es Google quien me está posicionando en los tópicos que trabajo. De todos modos, los diagramas y las redes tienen que seguir progresando si quieren competir con otras formas de representación diagramática, con otros modelos del razonamiento y espero poder seguir colaborando con otros lógicos, matemáticos y excelentes diseñadores gráficos como Pepe Amoedo en este proyecto.

JGR: Ya que mencionas la tesis, ¿Cómo explicarías en 30 segundos el tema de tu tesis?

MLA: Mi tesis, iniciada oficialmente en 2015, aunque se remonta la investigación a 2011, será defendida en 2020 y se titula “Diagramas lógicos de Marlo para el razonamiento visual y heterogéneo, válidos en lógica matemática y aristotélica”. En ella encontramos los diagramas de Marlo y las redes de Expectativas, herramientas para la didáctica de la lógica que pretenden ser útiles no solo a los alumnos con ventaja en el uso de números y fórmulas lógicas, sino a otro tipo de alumnos que razonan con colores, es decir, codificando la información con medios que habitualmente no empleamos en el aula y menos aún en las materias tradicionalmente relacionadas con el pensamiento abstracto.

JGR: ¿Cuáles son los puntos positivos y las dificultades que has encontrado durante esta etapa académica?

MLA: Lo más positivo que he encontrado al realizar la tesis doctoral ha sido la recepción de los académicos que han conocido mis diagramas, la retroalimentación que me han brindado, las ayudas, los consejos. Lo peor la sensación de ir descubriendo un océano cada vez mayor, el alejarse de la feliz ignorancia que me hacía sentir en 2014 que había descubierto algo muy original. Hoy sé, y es doloroso para mi ego, que Aristóteles, Boole y Jevons habían anticipado todos los principios que subyacen al diseño de mis diagramas. Pero a pesar de doler es también gratificante, porque me dan la razón los lógicos más importantes de todos los tiempos y porque eso significa que mis alumnos aprenden buena lógica con los diagramas, una sola lógica.

JGR: ¿Hay algo que te haya llamado la atención acerca de nuestra manera de aprender a lo largo de tus años de enseñanza?

MLA: Siempre he prestado atención al orden en el que tienen lugar los progresos cognitivos y la importancia de ver las cosas, de representar el conocimiento. Estoy convencido de que los caminos del aprendizaje deben ser materialmente señalizados. Debemos prestar atención a las curvas peligrosas, los terrenos resbaladizos. Por eso siempre le pido a mis alumnos que se expliquen apoyándose en imágenes, simplificando la información en esquemas y mediante el uso de ejemplos. Comprendemos lo que vemos y lo que somos capaces de conseguir que vean los demás de un modo claro y sencillo, por complejo que sea el contenido.

JGR: ¿Cuáles son los puntos fuertes de nuestro sistema de enseñanza?

MLA: El punto fuerte de todo proceso de transmisión de conocimiento es el vínculo profesor-alumno, la capacidad de señalar el uno al otro lo relevante, la corrección personalizada. Ese refuerzo pasa por disminuir la ratio en las aulas. No hay ninguna otra fórmula mágica. Todo esto de los recursos TIC, que yo mismo empleo como herramienta, deben ser siempre considerados como meros medios y no como un fin en sí mismos. No debemos confundir los medios y los fines. Hay que tener las metas claras y no olvidar que en el diseño de nuestros cerebros de mamíferos y primates el aprendizaje de la cultura es un fenómeno mediado por la relación de actores sociales, la imitación, la confianza, el trabajo codo a codo. Atiende a dónde te señalo aquí y ahora.

JGR: ¿Te gustaría compartir algún mensaje con los lectores?

MLA: Un docente nunca debería olvidar que si intenta explicar algo y el destinatario del mensaje no lo comprende tal vez es porque no está hablando en su mismo idioma. Es obligación del que comunica tratar de comprender el modo en el que la mente del receptor trabaja, el modo en el que aquél codifica y decodifica los mensajes. No puede el emisor tirar la toalla pensando que el estudiante tiene una inteligencia limitada. La razón se expresa de muchas maneras, tiene múltiples formas. He visto a un profesor de matemáticas humillar a una alumna porque se le daban mal los números. Y luego he visto a esa misma alumna llegar a las conclusiones lógicas en las redes y utilizando colores mucho antes que el resto de sus compañeros “matemáticamente eficientes”.  Da que pensar.

Referencias